Basics

Just like threshold AR(p) models, potential analysis in essence identifies flickering and serves as warning of the existence of alternative states. Potential analysis is a technique for deriving the shape of the underlying potential of a system. It assumes that a time series may be approximated by a stochastic potential equation

dZ = -[dU/dz]dt + σdW

where dU/dz is a polynomial potential of even order (2nd for one-well potential, 4th for double-well potential, etc.), dW is white noise of unit variance and intensity σ. The order of the best-fit polynomial in essence reflects the number of potential system states identified along the time series.

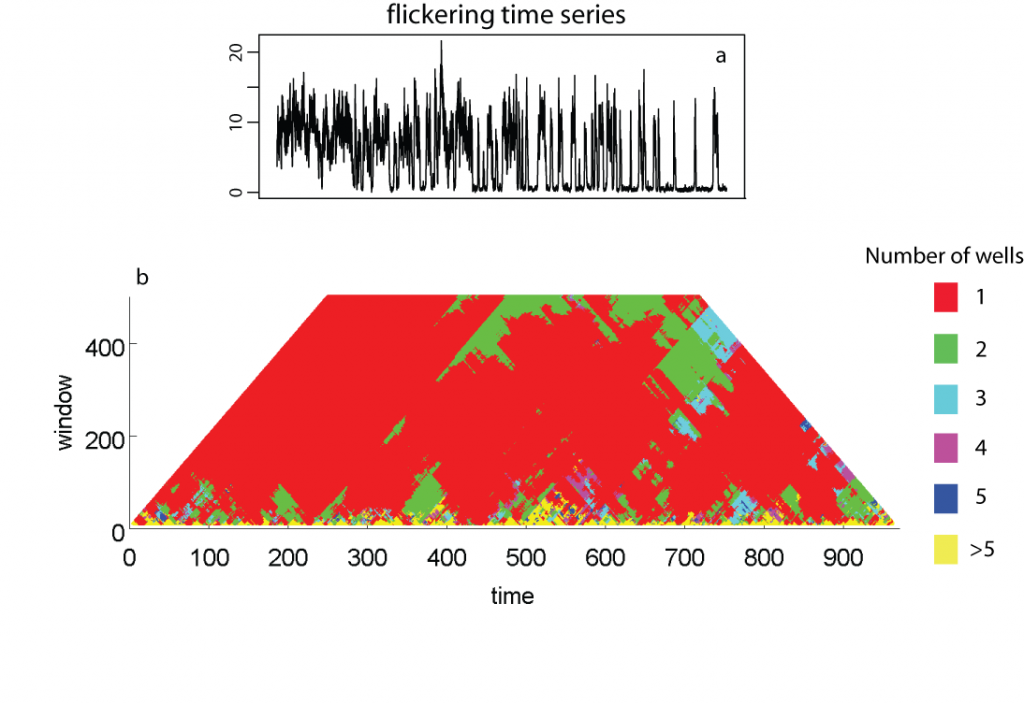
Example

Contrary to the threshold AR(p) model fitting, potential analysis is performed within rolling windows of different size (ranging from 10 to half the size of the dataset). We applied it on untransformed data for a flickering time series as we did for the threshold AR(p) models (panel a). We identified one state for most of the time series, except from the last 2,000 points onwards when multiple states where identified (panel b). Such high number of detected states meant that, in principle, the data were on the edge of having no clear potential.