Everyday examples illustrate that small changes in external conditions – like increasing pull to an elastic band – usually result in smoothresponses to the state of a system – the elastic band expands (panel a). Such a response is gradual, unsurprising, and reversible: once we relax the stretch, the elastic band regains its previous shape.

In other cases, small changes in conditions may cause disproportionally strong changes in the state of the system (panel b). Such marked responses around a threshold in conditions can still be continuous and reversible, in the sense that when conditions are restored to previous levels, the system returns to its former state.

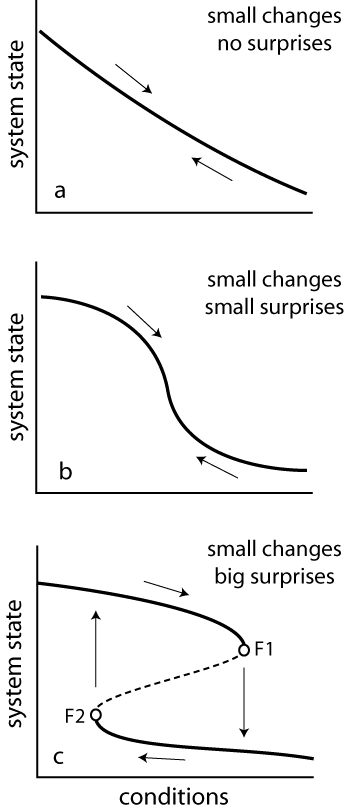
There are situations, however, where minute changes in conditions may trigger extreme discontinuous responses that are not easily reversible (panel c). This happens when at a threshold, the system abruptly shifts towards a contrasting state (threshold1 in panel c).

Such abrupt shifts triggered by small forces we describe as critical transitions. Mathematically, these critical transitions correspond to so-called catastrophic bifurcations. Catastrophic bifurcations are abrupt changes in the qualitative behavior of a system that occur at specific thresholds in external conditions (see Glossary). Catastrophic bifurcations arise in systems with alternative stable states (or, in general, alternative attractors, see Glossary): systems that may be in more than one different configurations under the same external conditions. For instance, the two branches in panel c represent two alternative stable states for the same range of conditions.